lunes, 5 de mayo de 2014

variables aleatorias discretas

Definición
Se denomina variable aleatoria discreta aquella que sólo puede tomar un número finito de valores dentro de un intervalo. Por ejemplo, el número de componentes de una manada de lobos, pude ser 4 ó 5 ó 6 individuos pero nunca 5,75 ó 5,87. Otros ejemplos de variable discreta serían el número de pollos de gorrión que llegan a volar del nido o el sexo de los componentes de un grupo familiar de babuinos.

Densidad
Se denomina densidad discreta a la probabilidad de que una variable aleatoria discreta X tome un valor numérico determinado (x). Se representa:
f(x) = P[X=x]
La suma de todas las densidades será igual a 1
{\sum_{todo_x} f(x)} = 1

DISTRIBUCIÓN DE PROBABILIDAD DE VARIABLES 
ALEATORIAS DISCRETAS 
 
ESPACIO MUESTRAL. El conjunto de todos los resultados posibles de un experimento estadístico 
denotado por “S” o “Ω ” 
 
VARIABLE. Se denomina variable a la entidad que puede tomar un valor cualesquiera durante la 
duración de un proceso dado. Si la variable toma un solo valor durante el proceso se llama constante. 
 
VARIABLE ALEATORIA: Es una función que asocia un número real a cada elemento del espacio 
muestral. Es decir son aquellas que pueden diferir de una respuesta a otra. 
 
Una variable aleatoria se puede clasificar en: 
 
 Variable aleatoria discreta. 
 
 Variable aleatoria continua. 
 
Variable aleatoria discreta. Una variable discreta proporciona datos que son llamados datos 
cuantitativos discretos y son respuestas numéricas que resultan de un proceso de conteo. 
 
La cantidad de alumnos regulares en un grupo escolar. 
El número de águilas en cinco lanzamientos de una moneda. 
Número de circuitos en una computadora. 
El número de vehículos vendidos en un día, en un lote de autos 
 
Variable aleatoria continua. Es aquella que se encuentra dentro de un intervalo comprendido entre dos 
valores cualesquiera; ésta puede asumir infinito número de valores y éstos se pueden medir. 
 
La estatura de un alumno de un grupo escolar. 
El peso en gramos de una moneda. 
La edad de un hijo de familia. 
Las dimensiones de un vehículo.



Distribución binomial


En estadística, la distribución binomial es una distribución de probabilidad discreta que cuenta el número de éxitos en una secuencia de n ensayos de Bernoulli independientes entre sí, con una probabilidad fija p de ocurrencia del éxito entre los ensayos. Un experimento de Bernoulli se caracteriza por ser dicotómico, esto es, sólo son posibles dos resultados. A uno de estos se denomina éxito y tiene una probabilidad de ocurrencia p y al otro, fracaso, con una probabilidad q = 1 - p. En la distribución binomial el anterior experimento se repite n veces, de forma independiente, y se trata de calcular la probabilidad de un determinado número de éxitos. Para n = 1, la binomial se convierte, de hecho, en una distribución de Bernoulli.
Para representar que una variable aleatoria X sigue una distribución binomial de parámetros n y p, se escribe:
X \sim B(n, p)\,


Ejemplos

Las siguientes situaciones son ejemplos de experimentos que pueden modelizarse por esta distribución:
  • Se lanza un dado diez veces y se cuenta el número X de tres obtenidos: entonces X ~ B(10, 1/6)
  • Se lanza una moneda dos veces y se cuenta el número X de caras obtenidas: entonces X ~ B(2, 1/2)

Experimento binomial

Existen muchas situaciones en las que se presenta una experiencia binomial. Cada uno de los experimentos es independiente de los restantes (la probabilidad del resultado de un experimento no depende del resultado del resto). El resultado de cada experimento ha de admitir sólo dos categorías (a las que se denomina éxito y fracaso). Las probabilidades de ambas posibilidades han de ser constantes en todos los experimentos (se denotan como p y q o p y 1-p).
Se designa por X a la variable que mide el número de éxitos que se han producido en los n experimentos.
Cuando se dan estas circunstancias, se dice que la variable X sigue una distribución de probabilidad binomial, y se denota B(n,p)

Características analíticas

\!f(x)={n \choose x}p^x(1-p)^{n-x} \,\!
donde x = \{0, 1, 2, \dots , n\},
siendo \!{n \choose x} = \frac{n!}{x!(n-x)!} \,\! las combinaciones de n \,\! en x \,\! (n \,\! elementos tomados de x \,\! en x \,\!)

Ejemplo

Supongamos que se lanza un dado (con 6 caras) 50 veces y queremos conocer la probabilidad de que el número 3 salga 20 veces. En este caso tenemos una X ~ B(50, 1/6) y la probabilidad sería P(X=20):
\!P(X=20)={50 \choose 20}(1/6)^{20}(1-1/6)^{50-20} \,\!

Propiedades

\mathbb{E}[X] = np\,
\mathbb{V}\text{ar}[X] =np(1-p)\,

Relaciones con otras variables aleatorias

Si n tiende a infinito y p es tal que el producto entre ambos parámetros tiende a \lambda \,\!, entonces la distribución de la variable aleatoria binomial tiende a una distribución de Poissonde parámetro \lambda.
Por último, se cumple que cuando p =0.5 y n es muy grande (usualmente se exige que n \geq 30 ) la distribución binomial puede aproximarse mediante la distribución normal.

Propiedades reproductivas

Dadas n variables binomiales independientes de parámetros ni (i = 1,..., n) y p, su suma es también una variable binomial, de parámetros n1+... + nn, y p, es decir,
Y = \sum^{n}_{i = 1} X_i \sim B(\sum^{n}_{i = 1} n_i, p)\,





Esperanza matemática

En estadística la esperanza matemática (también llamada esperanza, valor esperado, media poblacional o media) de una variable aleatoria  X , es el número \operatorname{E}[X] que formaliza la idea de valor medio de un fenómeno aleatorio.
Cuando la variable aleatoria es discreta, la esperanza es igual a la suma de la probabilidad de cada posible suceso aleatorio multiplicado por el valor de dicho suceso. Por lo tanto, representa la cantidad media que se "espera" como resultado de un experimento aleatorio cuando la probabilidad de cada suceso se mantiene constante y el experimento se repite un elevado número de veces. Cabe decir que el valor que toma la esperanza matemática en algunos casos puede no ser "esperado" en el sentido más general de la palabra - el valor de la esperanza puede ser improbable o incluso imposible.
Por ejemplo, el valor esperado cuando tiramos un dado equilibrado de 6 caras es 3,5. Podemos hacer el cálculo
\begin{align} \operatorname{E}(X) = 1 \cdot \frac{1}{6} + 2 \cdot \frac{1}{6} + 3 \cdot \frac{1}{6} + 4 \cdot \frac{1}{6} + 5 \cdot \frac{1}{6} + 6 \cdot \frac{1}{6}\\[6pt] = \frac{1 + 2 + 3 + 4 + 5 + 6}{6} = 3,5 \end{align}
y cabe destacar que 3,5 no es un valor posible al rodar el dado. En este caso, en el que todos los sucesos son de igual probabilidad, la esperanza es igual a la media aritmética.
Una aplicación común de la esperanza matemática es en las apuestas o los juegos de azar. Por ejemplo, la ruleta americana tiene 38 casillas equiprobables. La ganancia para acertar una apuesta a un solo número paga de 35 a 1 (es decir, cobramos 35 veces lo que hemos apostado y recuperamos la apuesta, así que recibimos 36 veces lo que hemos apostado). Por tanto, considerando los 38 posibles resultados, la esperanza matemática del beneficio para apostar a un solo número es:
\left( -1 \cdot \frac{37}{38} \right) + \left( 35 \cdot \frac{1}{38} \right),



que es -0,0526 aproximadamente. Por lo tanto uno esperaría, en media, perder unos 5 céntimos por cada euro que apuesta, y el valor esperado para apostar 1 euro son 0.9474 euros. En el mundo de las apuestas, un juego donde el beneficio esperado es cero (no ganamos ni perdemos) se llama un "juego justo".
Nota: El primer paréntesis es la "esperanza" de perder tu apuesta de 1€, por eso es negativo el valor. El segundo paréntesis es la esperanza matemática de ganar los 35€. La esperanza matemática del beneficio es el valor esperado a ganar menos el valor esperado a perder.

Definición

Para una variable aleatoria discreta con valores posibles x_1, x_2 \ldots x_n \,\! y sus probabilidades representadas por la función de probabilidad p(x_i) la esperanza se calcula como:
E[X]=x_1p(X=x_1)+...+x_np(X=x_n)=E[X]=\sum_{i=1}^{n} x_i p(x_i) \,\!
Para una variable aleatoria absolutamente continua, la esperanza se calcula mediante la integral de todos los valores y la función de densidad f(x) \,\!:
E[X]=\int_{-\infty}^\infty x f(x)dx \,\!
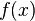La definición general de esperanza se basa, como toda la teoría de la probabilidad, en el marco de la teoría de la medida y se define como la siguiente integral:
\operatorname{E}[X] = \int_\Omega X\, \operatorname{d}P \,\!
La esperanza también se suele simbolizar con \mu = E[X] \,\!
Las esperanzas E[X^k] \,\! para k=0,1,2... \,\! se llaman momentos de orden k \,\!. Más importantes son los momentos centrados E[(X-E[X])^k] \,\!.
No todas las variables aleatorias tienen un valor esperado. Por ejemplo, la distribución de Cauchy no lo tiene.

Propiedades

Constantes

La esperanza matemática de una constante es igual a esa misma constante, es decir, si c es una constante, entonces E[c] = c.

Linealidad

La esperanza es un operador lineal, ya que:
\operatorname{E}[X + c]= \operatorname{E}[X] + c \,\!
\operatorname{E}[X + Y]= \operatorname{E}[X] + \operatorname{E}[Y] \,\! (*)
\operatorname{E}[aX]= a \operatorname{E}[X] \,\!
por ende:
\operatorname{E}[a X + b Y] = a \operatorname{E}[X] + b \operatorname{E}[Y] \,\!
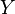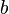donde X \,\! e Y \,\! son variables aleatorias y a \,\! y b \,\! son dos constantes cualesquiera.
Nótese que (*) es válido incluso si X no es independiente de Y.

Teorema de Bayes

En la teoría de la probabilidad el teorema de Bayes es un resultado enunciado por Thomas Bayes en 17631 que expresa la probabilidad condicional de un evento aleatorio Adado B en términos de la distribución de probabilidad condicional del evento B dado A y la distribución de probabilidad marginal de sólo A.
En términos más generales y menos matemáticos, el teorema de Bayes es de enorme relevancia puesto que vincula la probabilidad de A dado B con la probabilidad de B dado A. Es decir que sabiendo la probabilidad de tener un dolor de cabeza dado que se tiene gripe, se podría saber (si se tiene algún dato más), la probabilidad de tener gripe si se tiene un dolor de cabeza, muestra este sencillo ejemplo la alta relevancia del teorema en cuestión para la ciencia en todas sus ramas, puesto que tiene vinculación íntima con la comprensión de la probabilidad de aspectos causales dados los efectos observados.


Sea \{A_1, A_2, ..., A_i, ..., A_n\} un conjunto de sucesos mutuamente excluyentes y exhaustivos, y tales que la probabilidad de cada uno de ellos es distinta de cero (0). Sea B un suceso cualquiera del que se conocen las probabilidades condicionales P(B | A_i). Entonces, la probabilidad P(A_i | B) viene dada por la expresión:
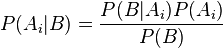P(A_i|B) = \frac{P(B | A_i) P(A_i)}{P(B)}
donde:
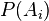  • P(A_i) son las probabilidades a priori.
  • P(B|A_i) es la probabilidad de B en la hipótesis A_i.
  • P(A_i|B) son las probabilidades a posteriori.


Fórmula de Bayes

Con base en la definición de Probabilidad condicionada, obtenemos la Fórmula de Bayes, también conocida como la Regla de Bayes:
P(A_i|B) = \frac{P(B | A_i) P(A_i)}{\sum_{k=1}^n P(B | A_k) P(A_k)}

Aplicaciones

El teorema de Bayes es válido en todas las aplicaciones de la teoría de la probabilidad. Sin embargo, hay una controversia sobre el tipo de probabilidades que emplea. En esencia, los seguidores de la estadística tradicional sólo admiten probabilidades basadas en experimentos repetibles y que tengan una confirmación empírica mientras que los llamados estadísticos bayesianos permiten probabilidades subjetivas. El teorema puede servir entonces para indicar cómo debemos modificar nuestras probabilidades subjetivas cuando recibimos información adicional de un experimento. La estadística bayesiana está demostrando su utilidad en ciertas estimaciones basadas en el conocimiento subjetivo a priori y el hecho de permitir revisar esas estimaciones en función de la evidencia empírica es lo que está abriendo nuevas formas de hacer conocimiento. Una aplicación de esto son los clasificadores bayesianos que son frecuentemente usados en implementaciones de filtros de correo basura o spam, que se adaptan con el uso.
Como observación, se tiene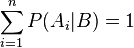 \sum_{i=1}^{n}P(A_i |B)=1 y su demostración resulta trivial.

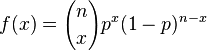
Publicadas por a la/s

No hay comentarios.:

Publicar un comentario

Suscribirse a: Comentarios de la entrada (Atom)